Stereograms - technical description

by W.A. Steer PhD
Back to contents About...

A technical description of autostereograms, their geometry, and the algorithms and programs I developed for creating them.

Previous Algorithms

Some of the early single-image stereograms were created by drawing for each line (say 50) random dots starting at the left-hand side of the screen, then continuing the pattern by copying the 51st dot from the 1st dot, 52nd from 2nd etc. However, the `lookback distance', initially 50 pixels, was then varied down to a minimum of 30 dots or so according to the depth to be represented. Shorter lookback distances correspond to shallower depth in the 3D image.

While these demonstrated that a single-image stereogram was possible, there are three major problems with this empirical method:

depth is non-linear
it is asymmetric - the 3D image gets skewed sideways by an amount dependent on its depth
spurious 3D image fragments become introduced which repeat or 'echo' across the rest of the scene.

These limitations can be overcome by studying the underlying geometry and adopting a more rigorous approach. I have taken as a starting point the core of the symmetric algorithm documented in "Displaying 3D Images: Algorithms for Single Image Random Dot Stereograms" by H.W. Thimbleby, S. Inglis and I.H. Witten. Readers of that paper will notice that I have used a more intuitive coordinate system, and should note that I develop my own hidden-surface and anti cross-linking methods which supercede earlier approaches.

Geometry used in the algorithms presented

Consider a transparent screen placed between an observer and a three-dimensional object. When the observer looks at a particular point on the object two rays can be drawn from that point, one to each eye (see figure 1). The rays to the left and right eyes clearly pass through a different place on the screen. For parts of the object that are close to the screen the separation will be smaller than for more distant points.

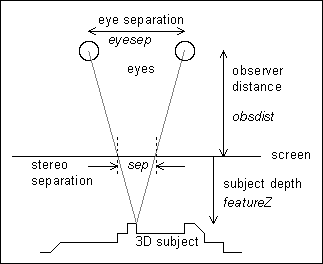
Line-diagram of geometrical setup, defining the variables used later.
Figure 1: Geometry.

This "stereo separation" at the screen can be quantified by applying similar triangles, and assuming that the point on the object is straight ahead of the viewer:

   sep = (eyesep * featureZ) / (featureZ + obsdist)         [equation 1]

Conversely, two similarly coloured points placed on the screen at this separation can represent a virtual point behind the screen. In this way it is possible to create an "autostereogram" which when suitably viewed, by diverging the eyes as if looking through the screen, reveals a 3D image.

Note that equation 1 is absolutely central to the process of generating stereograms with linear depth. Later references to z-resolution and permissable depths of field etc. are derived from that expression.

Method for creating random dot stereograms (RDS)

The general method adopted is as follows:

Start with a "depth-map" - array of z-values for each (x,y) point on the screen.
Working left to right along each horizontal line, for each point on the depth-map identify the associated pair of screen points and `link' them - give each a reference to its other half.
Again working from left to right, assign a random colour to each unlinked point, and colour linked points according to the colour of their (already coloured) other half.

Programs

To maximise drawing speed, especially on older hardware, I have avoided the use of floating point maths in the main program loop. Depths, heights and widths are measured in pixels.

To start with, each point is `linked' to itself, purely to indicate that it is not linked to any other. Proper links are then calculated, working from left to right. Links are only recorded if both the left and right points are within the bounds of the picture, and are one way, i.e. the right-hand point of each pair references the left in the array lookL[], but not vice-versa. This is sufficient (at this stage) as we apply the random dots from left to right also.

 const maxwidth=640;
 int xdpi=75;    // x-resolution of typical monitor

 int width=640;  // width of display in pixels
 int height=480; // height of display in pixels

 int lookL[maxwidth];
 COLOUR colour[maxwidth]; // any type suitable for storing colours

 int obsDist=xdpi*12;
 int eyeSep=xdpi*2.5;

 int featureZ, sep;
 int x,y, left,right;

 for (y=0; y<height; y++)
 {
  for (x=0; x<width; x++)
  { lookL[x]=x; }

  for (x=0; x<width; x++)
  {
   featureZ=<depth of image at (x,y)>; // insert a function or
				       // refer to a depth-map here

   // the multiplication below is 'long' to prevent overflow errors

   sep=(int)(((long)eyeSep*featureZ)/(featureZ+obsDist));

   left=x-sep/2; right=left+sep;

   if ((left>=0) && (right<width)) lookL[right]=left;
  }

The second stage is to apply the pattern within the constraints imposed by the links. This is quite simple and the program speaks for itself (random-dot method):

  for (x=0; x<width; x++)
  {
   if (lookL[x]==x)
    colour[x]=<random colour>; // unconstrained
   else
    colour[x]=colour[lookL[x]]; // constrained
  }

The third stage is to plot the resulting pattern on screen.

  for (x=0; x<width; x++)
  {
   SetPixel(x,y, colour[x]);
  }
 }

Selecting the depth and depth range for a stereogram

The range of depths used in a stereogram should be chosen carefully for the following reasons:

It is very unwise to have a range of depths that causes the stereo separation to vary by a factor approaching two or more. Failure to adhere to this restriction means that twice the near repeat-width is of comparable magnitude to the whole far repeat-width, and misconvergence often results, making the picture difficult to see.
Within the first constraint, it is soon apparent from the depth-separation formula that the allowable depth of field (range of depths) is much greater on deeper pictures (see graph).
Z-resolution decreases with increasing depth (see graph), but note that the z-resolving power of the eyes decreases in proportion.
Very shallow stereograms naturally have narrow repeat widths and it is easy to look deeper than necessary, by diverging the eyes over two or more repeats for example. While the effect may be "interesting", it is certainly not desirable.

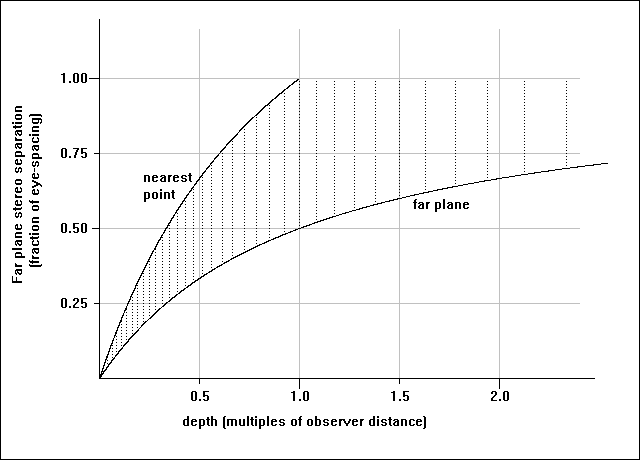
Line graph
Graph 1: relation between stereogram depths and depth of field. The dotted vertical lines show discrete depths representable with a 20dpi display, and indicate the reduction of z-resolution with increasing depth.

Generally, a good starting point is to make the maximum depth equal to the observer distance. This gives a maximum stereo separation of half an eye-separation on which it is almost impossible to mis-converge the eyes, and permits the uninitiated to use their reflection from the surface as a guide.

From equation (1) it can be shown that the minimum permissible depth in the stereogram consistent with the first rule is given by:

  mindepth=(sepfactor*maxdepth*obsdist)/((1-sepfactor)*maxdepth+obsdist)

where sepfactor is the ratio of the smallest allowable separation to the maximum separation used. A typical value would be 0.55.

Of course in any particular stereogram the shallowest depth used does not have to be the absolute minimum allowable.

If the stereogram depth information will be obtained from a ray-tracer then it is a good idea to create the original scene with these constraints in mind, then the co-ordinate systems of the two processes can easily be interchanged and correct perspective obtained.

In that case, use:

  featureZ=<distance of point behind screen according to ray tracer>

Alternatively, if a depth-map height-function is used then the following formula should be used:

  featureZ=maxdepth-h(x,y)*(maxdepth-mindepth)/256

where h(x,y) is a height function with values from 0 (farthest) to 255 (nearest). h may be obtained from a grey scale depth-map picture,
maxdepth is the farthest depth (corresponding to 0 in the height function), and
mindepth is the nearest depth, (corresponding to 255 in the height function).

The need for hidden-surface removal

Stereograms created using the program above will exhibit artifacts if the corresponding depth-map has `steps' - abrupt changes in depth as you move across the image. To the immediate right of any step that becomes deeper as you go rightwards there will hang a thin (depending on the size of the step) `flange' at the nearer depth. More seriously this artifact will repeat periodically rightwards across the rest of the picture. (In fact any slope which is so steep that it is visible only to the right eye will become distorted, but this is less apparent).

The problem arises because links are made even for points on the object that are only visible to one eye. In the case of the depth getting shallower in a rightwards direction, incorrect links tend to be overwritten with good ones. When the depth gets deeper rightwards, bad links overwrite good. The resulting mixture of good and bad links means that some `left' points can be referred to by two or more `right' points. Such double-linking leads to depth-ambiguities (the `flange'), and because the stereogram process can only correctly support unique depths, the flange becomes repeated with the rest of the pattern and spoils the picture.

The foolproof solution is to prevent links being made for points that are visible to only one eye - hidden surface removal. Previous hidden-surface algorithms essentially trace the path of the ray from the object to the eye and check that it never passes behind the surface of the object. If it does then that ray is deemed to be broken, the view of the point obscured, and no link made. However, this method is very slow.

Given that:

near objects obscure far ones
stereo separation increases with depth

we can conclude that short links should always be made in preference to longer ones (see figure 2). This algorithm is easier to program, and the code runs much faster.

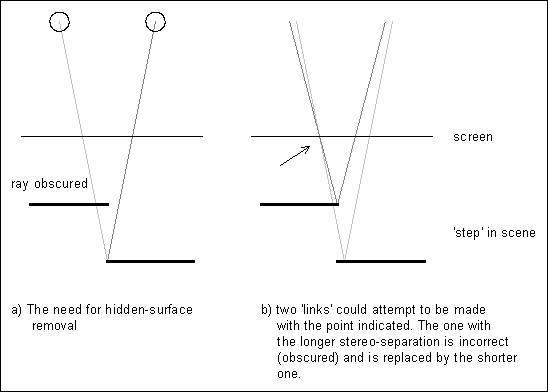
Line-diagram showing geometry utilised for hidden-surface routine
Figure 2: Hidden surface removal.

To permit quick investigation of already-formed links, I have introduced a second look[] array, lookR[], to directly record the links in a rightwards direction. Before forming each link, a check is made as to whether the left or right points already have shorter links, if so, no new link is made. Otherwise any longer links are removed (this involves finding the other halves, and cancelling their look[] too) and the new link made.

Add the following two lines at the start of the program

 int lookR[maxwidth];
 BOOL vis;

and amend the contents of the first two for(x=...) loops as shown

  for (x=0; x<width; x++)
  { lookL[x]=x; lookR[x]=x; }    // clear lookR[] as well

  for (x=0; x<width; x++)
  {
   featureZ=<depth of image at (x,y)>; // insert a function or
                                       // refer to a depth-map here

   sep=(int)(((long)eyeSep*featureZ)/(featureZ+obsDist));

   left=x-sep/2; right=left+sep;

   vis=TRUE;  // default to visible to both eyes

   if ((left>=0) && (right<width))
   {
    if (lookL[right]!=right) // right pt already linked
    {
     if (lookL[right]<left) // deeper than current
     {
      lookR[lookL[right]]=lookL[right]; // break old links
      lookL[right]=right;
     }
     else vis=FALSE;
    }
     
    if (lookR[left]!=left) // left pt already linked
    {
     if (lookR[left]>right) // deeper than current
     {
      lookL[lookR[left]]=lookR[left]; // break old links
      lookR[left]=left;
     }
     else vis=FALSE;
    }
    if (vis==TRUE) { lookL[right]=left; lookR[left]=right; } // make link
   }
  }

For all practical purposes my method of hidden surface removal is at least as good as any other, and much faster. In fact because it works directly on the links it is absolutely guaranteed to prevent multiple links and the associated artifacts. With traditional hidden surface algorithms there is always the chance that rounding errors will allow a few multiple links to slip through. Recall that we originally specified the depth as an array of unique z-values, z(x,y). It is usual when programming the older hidden surface removal method to assume the scene extends from the defined points all the way back to infinity. In contrast, my method effectively takes the scene as comprising only sections of planes parallel to the screen as defined in the array. In extreme geometrical cases (e.g. object less than a quarter of an inch wide in front of a background some 7 inches or more behind) it would be possible observe some of the background to either side of the object with the ray to one eye going behind the object (see figure 3). The background directly behind the object, though technically visible to both eyes, is inherently given undefined depth by the algorithm described and might appear as a hole in the background. This situation is extremely rare, and still does not cause any other defects in the image.

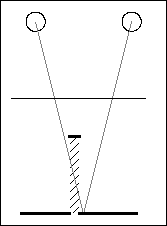
Line diagram
Figure 3: Extreme geometrical case where it is revealed that the scene does not extend back to infinity from the front surfaces.

Limitations of RDS

By now, you should have observed that depth in simple stereograms as described is not smooth. Slopes appear as steps and curved objects appear to be made from a stack of flat planes. As a guide, for depths from a half- to one viewer distance, z-resolution is of the order of 7 to 10 times coarser than the x-resolution of the display device. Smoother stereograms appear much more solid and convincing. Using a higher definition display is a brute-force solution, and particularly suitable for laser printers. But a pattern of random dots 600 to the inch looks like an even grey mass and the stereogram is very difficult to see because there is no large-scale detail. Various tricks can be played, like positioning larger dots to the finer resolution, but a more pleasing technique is to use a pattern or picture rather than random dots as the basis for the stereogram. Fortunately resolution-enhancement techniques (see below) lend themselves to such patterns and can be applied to give smooth pictures even on an ordinary monitor. RDS techniques can be adapted for resolution-enhancement, but results still tend to be mediocre because of the lack of large-scale detail.

Using bitmapped patterns

Generally in a stereogram there is a broad vertical strip consisting entirely of unconstrained points, usually at the left-hand edge. With mutations imposed by the constraints, this strip is effectively duplicated across the whole screen. To add interest and make viewing much easier you can start with a bitmapped picture or pattern rather than random-dots.

The pattern must be at least as wide as the maximum stereo separation otherwise there is a problem. You cannot just loop around and begin the pattern again because the repeat will be interpreted by the observer as three-dimensional information and artifacts will result - visible fragments of 3D surfaces that weren't supposed to be there. If the chosen pattern is designed to "tile" then to optimise the matching the stereogram paramters can be adjusted and/or the pattern resized in advance so that the pattern width is equal to the maximum stereo separation.

When applying the pattern from left to right, new pixels have to be inserted where parts of the object are seen by the right eye only. These regions of the picture have undefined depth, but given no other information the brain often associates them with the farther depth (this occurs with RDS). However, there can be a problem with patterned stereograms if the new pattern obviously doesn't match up: lone inserted pixels tend to float and twinkle, and larger sections may appear as a "hole" in the image. There is no easy solution to the "hole" problem, although its severity depends on the pattern used, and tends only to be a problem if you look for it!

In reality, a gently receding slope is visible to both eyes, though one eye will see the surface detail slightly stretched compared to the other. For the stereogram where smooth slopes have been quantized as a sucession of many flat sections, there will be a lone pixel visible only to one eye inserted on the edge on the edge of each step. It is these which can twinkle if new colours are used because the brain expects both eyes to be seeing the same thing, albeit with a small distortion, and "retinal rivalry" occurs. My solution to this problem is to copy the colour of an adjacent pixel in these circumstances.

At real depth-disjoints in the 3D image it is necessary to insert new sections of pattern. However these must not duplicate pattern already used on that line of the stereogram otherwise artifacts arise in the 3D scene akin to those we removed with hidden surface removal. I chose to fill-in using pattern taken from a number of lines higher or lower than the current line. Experiment showed that vertical offsets in increments of 1/16th inch are quite adequate to prevent the observer's brain making incorrect associations, and hence eliminate artifacts.

A few new variables and arrays are introduced at the start of the program:

 int ydpi=75;
 int yShift=ydpi/16;
 int patHeight=patternbmp->GetHeight();

 int maxdepth=12*xdpi; // maximum depth used

 int maxsep=(int)(((long)eyeSep*maxdepth)/(maxdepth+obsDist)); // pattern must be at
                                                               // least this wide
 int lastlinked;

The linking and plotting processes are identical to last time, but the third (pattern-applying) for(x...) loop is replaced by that below which uses the pattern rather than random-dots.

  lastlinked=-10; // dummy initial value

  for (x=0; x<width; x++)
  {
   if (lookL[x]==x)
   {
    if (lastlinked==(x-1)) colour[x]=colour[x-1];
    else
    {
     colour[x]=GetPixelFromPattern(x % maxsep,
                                   (y+(x/maxsep)*yShift) % patHeight);
    }
   }
   else
   {
    colour[x]=colour[lookL[x]];
 
    lastlinked=x; // keep track of the last pixel to be constrained
   }
  }

where

GetPixelFromPattern(x,y) is a function that returns the colour of the pixel at (x,y) within the original pattern bitmap.

patternbmp->GetHeight() returns the height of the pattern in pixels.

Experiment using different patterns, Windows wallpapers for example, or scanned pictures or photographs. They have a dramatic effect on the appearance of the stereogram. For large, generally smooth and recognisable 3D subjects you can get away with many types of pattern. However, you will find that patterns with much fine detail are needed to reproduce subtle shapes and depth changes.

Resolution enhancement - at last!

The easiest way to implement resolution-enhancement is to process each line of the stereogram at a resolution several times greater than that of the display device, then merge a number of `virtual' pixels into each physical pixel for display. In this way each physical pixel takes on the average colour of its associated `virtual' pixels. Obviously this slows down the processing, but the results are worthwhile. Calculation (or simple practical experiment) shows that the resolution of the human eye at a typical reading distance (14 inches) does not exceed about 300dpi. Hence it is a waste of effort to calculate a stereogram with either real or virtual resolution in excess of this figure. By the same token, assuming that in any reasonable stereogram the stereo separation does not vary by more than one inch, it is humanly impossible to resolve more than approximately 300 depths in that range. Computationally it is convenient to set the limit at 256 depths, as suggested earlier.

New variables:

  oversam	= oversampling ratio ie. ratio of virtual pixels to real pixels
  vwidth	= the new `virtual' width
  veyeSep	= eye separation in `virtual' pixels
  vmaxsep	= maximum stereo separation in 'virtual' pixels

Here is the full program:

 int patHeight=patternbmp->GetHeight();

 const maxwidth=640*6;  // allow space for up to 6 times oversampling
 int xdpi=75; int ydpi=75;

 int yShift=ydpi/16;

 int width=640;
 int height=480;

 int oversam=4; // oversampling ratio
 int lookL[maxwidth]; int lookR[maxwidth];
 COLOUR colour[maxwidth], col;
 int lastlinked; int i;

 int vwidth=width*oversam;

 int obsDist=xdpi*12;
 int eyeSep=xdpi*2.5; int veyeSep=eyeSep*oversam;

 int maxdepth=xdpi*12;
 int maxsep=(int)(((long)eyeSep*maxdepth)/(maxdepth+obsDist)); // pattern must be at
                                                               // least this wide
 int vmaxsep=oversam*maxsep

 int featureZ, sep;
 int x,y, left,right;
 BOOL vis;
 

 for (y=0; y<height; y++)
 {
  for (x=0; x<vwidth; x++)
  { lookL[x]=x; lookR[x]=x; }

  for (x=0; x<vwidth; x++)
  {
   if ((x % oversam)==0) // SPEEDUP for oversampled pictures
   {
    featureZ=<depth of image at (x/oversam,y)>

    sep=(int)(((long)veyeSep*featureZ)/(featureZ+obsDist));
   }

   left=x-sep/2; right=left+sep;

   vis=TRUE;

   if ((left>=0) && (right<vwidth))
   {
    if (lookL[right]!=right) // right pt already linked
    {
     if (lookL[right]<left) // deeper than current
     {
      lookR[lookL[right]]=lookL[right]; // break old links
      lookL[right]=right;
     }
     else vis=FALSE;
    }

    if (lookR[left]!=left) // left pt already linked
    {
     if (lookR[left]>right) // deeper than current
     {
      lookL[lookR[left]]=lookR[left]; // break old links
      lookR[left]=left;
     }
     else vis=FALSE;
    }
    if (vis==TRUE) { lookL[right]=left; lookR[left]=right; } // make link
   }
  }

  lastlinked=-10; // dummy initial value

  for (x=0; x<vwidth; x++)
  {
   if (lookL[x]==x)
   {
    if (lastlinked==(x-1)) colour[x]=colour[x-1];
    else
    {
     colour[x]=GetPixelFromPattern((x % vmaxsep)/oversam,
                                   (y+(x/vmaxsep)*yShift) % patHeight);
    }
   }
   else
   {
    colour[x]=colour[lookL[x]];
 
    lastlinked=x; // keep track of the last pixel to be constrained
   }
  }

  int red, green, blue;

  for (x=0; x<vwidth; x+=oversam)
  {
   red=0; green=0; blue=0;
   
   // use average colour of virtual pixels for screen pixel
   for (i=x; i<(x+oversam); i++)
   {
    col=colour[i];
    red+=col.R;
    green+=col.G;
    blue+=col.B;
   }
   col=RGB(red/oversam, green/oversam, blue/oversam);

   SetPixel(x/oversam,y, col);
  }
 }

Note that the depth information required (in the featureZ= line) is still measured in units of the width of a whole pixel.

Resolution enhancement makes stereograms quite acceptable on an ordinary medium-resolution monitor by smoothing away the harsh depth-steps. To achieve ultimate high-definition and greater clarity stereograms still need to be created for better resolution display devices (such as laser printers).

Practical points on the use of in-between colors

If the display device supports 15- or 24-bit colour (32768 or 16.7million colours) then displaying in-between colours presents no difficulty. However, many common displays use a palette of just 256 colours. Provided there is a good tonal range in the palette of the original pattern then the nearest available colour can be used in place of the ideal in-between. The process of matching nearest colours is intrinsically slow; the required calls to Windows' built-in GetNearestPaletteIndex() function can take considerably more processor time than the stereogram maths! In practice, to reduce the time taken, a lookup table would be used (by limiting the colour to 15-bit, only 32768 bytes are needed) - see special topics on colour matching and other speedups.

And finally...

When the pattern is applied by working from one side to the other (left to right for example), the pattern can become very distorted on the far side of the picture. Although the 3D effect is not affected, the page assumes an asymmetric appearance. The total distortion can be reduced by using a from-the-centre-outwards approach: start with the original pattern in a vertical stripe down the centre, and mutate the pattern towards the edges. This also gives a much more pleasing `balanced' appearance to the work, but requires separate coding for left-to-right and right-to-left pattern application.

 int patHeight=patternbmp->GetHeight();

 const maxwidth=640*6;  // allow space for up to 6 times oversampling
 int xdpi=75; int ydpi=75;

 int yShift=ydpi/16;

 int width=640;
 int height=480;

 int oversam=4; // oversampling ratio
 int lookL[maxwidth]; int lookR[maxwidth];
 COLOUR colour[maxwidth], col;
 int lastlinked; int i;

 int vwidth=width*oversam;

 int obsDist=xdpi*12;
 int eyeSep=xdpi*2.5; int veyeSep=eyeSep*oversam;

 int maxdepth=xdpi*12;
 int maxsep=(int)(((long)eyeSep*maxdepth)/(maxdepth+obsDist)); // pattern must be at
                                                               // least this wide
 int vmaxsep=oversam*maxsep

 int s=vwidth/2-vmaxsep/2; int poffset=vmaxsep-(s % vmaxsep);

 int featureZ, sep;
 int x,y, left,right;
 BOOL vis;
 

 for (y=0; y<height; y++)
 {
  for (x=0; x<vwidth; x++)
  { lookL[x]=x; lookR[x]=x; }

  for (x=0; x<vwidth; x++)
  {
   if ((x % oversam)==0) // SPEEDUP for oversampled pictures
   {
    featureZ=<depth of image at (x/oversam,y)>

    sep=(int)(((long)veyeSep*featureZ)/(featureZ+obsDist));
   }

   left=x-sep/2; right=left+sep;

   vis=TRUE;

   if ((left>=0) && (right<vwidth))
   {
    if (lookL[right]!=right) // right pt already linked
    {
     if (lookL[right]<left) // deeper than current
     {
      lookR[lookL[right]]=lookL[right]; // break old links
      lookL[right]=right;
     }
     else vis=FALSE;
    }

    if (lookR[left]!=left) // left pt already linked
    {
     if (lookR[left]>right) // deeper than current
     {
      lookL[lookR[left]]=lookR[left]; // break old links
      lookR[left]=left;
     }
     else vis=FALSE;
    }
    if (vis==TRUE) { lookL[right]=left; lookR[left]=right; } // make link
   }
  }

  lastlinked=-10; // dummy initial value

  for (x=s; x<vwidth; x++)
  {
   if ((lookL[x]==x) || (lookL[x]<s))
   {
    if (lastlinked==(x-1)) colour[x]=colour[x-1];
    else
    {
     colour[x]=GetPixelFromPattern(((x+poffset) % vmaxsep)/oversam,
                                   (y+((x-s)/vmaxsep)*yShift) % patHeight);
    }
   }
   else
   {
    colour[x]=colour[lookL[x]];
 
    lastlinked=x; // keep track of the last pixel to be constrained
   }
  }

  lastlinked=-10; // dummy initial value

  for (x=s-1; x>=0; x--)
  {
   if (lookR[x]==x)
   {
    if (lastlinked==(x+1)) colour[x]=colour[x+1];
    else
    {
     colour[x]=GetPixelFromPattern(((x+poffset) % vmaxsep)/oversam,
                                (y+((s-x)/vmaxsep+1)*yShift) % patHeight);
    }
   }
   else
   {
    colour[x]=colour[lookR[x]];
 
    lastlinked=x; // keep track of the last pixel to be constrained
   }
  }

  int red, green, blue;

  for (x=0; x<vwidth; x+=oversam)
  {
   red=0; green=0; blue=0;
   
   // use average colour of virtual pixels for screen pixel
   for (i=x; i<(x+oversam); i++)
   {
    col=colour[i];
    red+=col.R;
    green+=col.G;
    blue+=col.B;
   }
   col=RGB(red/oversam, green/oversam, blue/oversam);

   SetPixel(x/oversam,y, col);
  }
 }

Special topic: Speedups

Once any program works well, there is always the desire to make it run faster. I found that on a 20MHz 486sx computer running Windows my original programs took about 5 minutes to draw a 640x480-pixel 2 times oversampled stereogram. With some general- and some machine-specific speedups (and not yet recourse to hand-crafted machine code) that time has now been slashed to under 20 seconds!

I cannot resist hinting at how I achieved some dramatic speedups, and hope to whet your appetite for the subject (which seems to be sadly neglected by many of the main-stream software companies!).

Microseconds count in the innermost loops where code may be executed over a million times. For the outer "for y..." loop, performed only hundreds of times, speed is less of an issue. Hence it always makes sense to optimise deepest loops first. Be aware that some speedups sacrifice clarity of program and may complicate any future changes to the algorithm. Note also that some speedups, particularly buffers, may decrease the performance in some circumstances. I try to balance speed against simplicity. There also comes a point when the law of diminishing returns sets in. It is easy to spend many hours of programming time trying to shave just fractions of a second off the run time!

The following give a taste of some specific speedups used in the latest version of SISGen:

Colour palette matching: - a major speedup for palette-based displays. If the display device supports 15- or 24-bit colour (32768 or 16.7million colours) then displaying in-between colours presents no difficulty. In reality though, common displays use a palette of just 256 colours. Provided there is a good tonal range in the palette of the original pattern then the nearest available colour can be used in place of the ideal in-between. However, the process of matching nearest colours is intrinsically slow; prior to optimisation in my program, calls to Windows' built-in GetNearestPaletteIndex() accounted for 60% of the run-time! In SISgen, I quantised the specification of each requested colour to 15-bit (5-bits per R/G/B channel), and implemented a lookup-table buffer to store the results of previous matches. That way, the best palette-entry for a particular colour only has to be found once in the drawing of the whole stereogram.
Integer maths: - on general purpose computers without math co-processors, integer maths is much faster than floating point. (On my PC I estimate a standard float multiplication to take around 100 times longer than the equivalent 16-bit integer operation.) Consequently the program was written in such a way that no floating point was required within the main loops.
In my latest program I have eliminated almost all maths in the main loop anyway by using a lookup table to relate image depth to stereo separation.
GetPixel()- and SetPixel()-type calls: Built-in pixel manipulation functions in most computer languages are often much slower than they need be - important as a stereogram may easily involve the order of a million calls! It may well be worth writing your own (see below).
Machine-specific optimization.: I found that it is approaching 10 times faster under Microsoft Windows to directly manipulate 256-colour device-independant bitmaps than to use the built-in pixel-manipulation functions on standard (device-specific) bitmaps.
Finally, make sure any compiler options are set to optimise for fast execution - and time it - sometimes the compiler gets it wrong!

Notes

With the exception of the linking routine documented in the paper by S. Inglis et. al. (for which permission for use has been granted) and used with modifications, the above is entirely my own work.

All C code is taken from working programs. However, the programs needed a degree of processing before landing on this page, so it is concievable that a couple of minor errors could have crept in! If you do find a problem, let me know!

Corrections made 1 July 1996

lastlinked inital values

In the program listings initial dummy values of variable lastlinked were changed to -10. For the programs which apply pattern leftwards only, starting from x=0, the former value of -1 caused problems (figure out why!). - Thanks to Stephane Defreyne for bringing this one to my attention.

Integer overflow error

In the listings for patterned stereograms, the calculation in the definition of the variable maxsep would have caused an integer overflow. It has now been ammended to read:

 int maxsep=(int)(((long)eyeSep*maxdepth)/(maxdepth+obsDist)); // pattern must be at
                                                               // least this wide

with the required long type-casting. - Thanks to Armando for pointing that one out.

Pattern-copying slip-up!

In the final listing, the loop which applies pattern leftwards from the mid-way start now reads:

for (x=s-1; x>=0; x--)
{
 if (lookR[x]==x)
 {
  ...
 }
 else
 {
  colour[x]=colour[lookR[x]];
  lastlinked=x;
 }
}

- obviously(?)! - Thanks again to Armando.

All three errors probably occurred at times when these listings were ammended to reflect improvements and simplifications made in my working Windows source code.

Originally written: 1995
Last modified: 12 June 2002
Source: http://www.techmind.org/stereo/stech.html