by W.A. Steer PhD
![]()
by W.A. Steer PhD
| Back to contents | About... |
![]()
Standard PC multimedia audio facilities offer much under-utilised potential for both scientific and simply amusing projects. I present a ready-to-run experimental soundcard-based software frequency-counter/instrument tuner, real-time spectrum analyser, and a sinewave signal generator, all for use at frequencies up to 20kHz. I've also outlined some attempts to characterise the frequency response and resonances of a speaker and microphone system - with the aim of generating a digital filter to remove the worst imperfections, and progress with an 'acoustic radar'.
From this starting point, I have developed several audio applets - see below.
The applets don't need any fancy installation, won't touch your Windows Registry, amd won't install any DLLs. Just download the .EXEs and run them. All require Windows 95 or later.
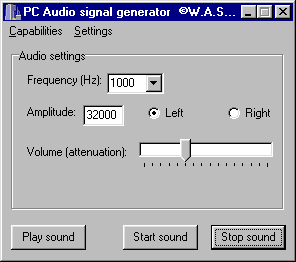
Select or enter a frequency (1 to 22050Hz), an amplitude (1 to 32767), choose left or right channel for output. Press 'play sound' for a one-second burst, or 'start-' and 'stop sound' to control the sound continuously (up to a limit of 10 hours!). The Volume slider should duplicate the Wave volume control on your sound-out mixer panel. If the sound is playing, then changes (except the Volume slider) won't be heard until the sound is stopped and restarted.
Download: siggen.exe This version is superceeded
Download: SigGen_1v3.exe New version 1.3, available
since May 2011. Supports multiple soundcards and better-matched to Windows Vista/7 sound models.
By downloading these files, you consent to the standard disclaimer.
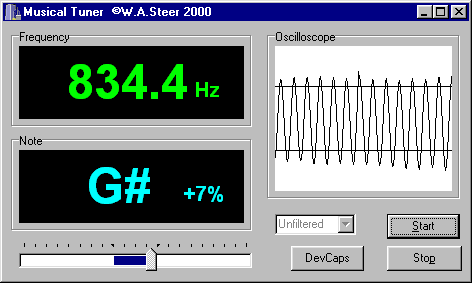
The tuner samples the currently selected audio-in (set by your 'Recording' volume control panel) in one-tenth second chuncks. It then counts the number of complete wavecycles and divides by the time taken to obtain the frequency. The frequency is displayed in the top left, and is expressed as the nearest musical note plus or minus so-many cents (according to an equally tempered scale based on A as 440.0Hz).
The display is bright when the program believes it has a self-consistent reading. If the volume is too low (or fluctuating too much), the signal is rich in harmonics, or contaminated by extraneous sounds or electrical interference, then the display remains dim. If the signal is too loud then the display goes red.
Performance can be greatly improved by using some kind of narrow-band digital filter (perhaps adaptively) tuned to the frequency of interest. This practically eliminates the problem of harmonics affecting the reading. While I've done it experimentally, this feature is not yet ready for general release!
New program version 1.3, below, really fixes the earlier division-by-zero errors issue!
Download: tuner1v3.exe [from 20 July 2005, released March 2012]
By downloading this file, you consent to the
standard disclaimer.
where f is in Hertz and n is an integer, as follows:
0 1 2 3 4 5 6 7 8 9 10 11 A A# B C C# D D# E F F# G G#to n, add multiples of 12 to reach higher octaves, or subtract multiples of 12 for lower octaves.
Because it measures the actual time of one (or more) complete waveforms and doesn't merely "count" cycles within the measurement period, you can get accurate results even when only counting a small number of impulses. I've dropped the sampling rate to 22050Hz and doubled the buffer length, so the sampling period is now 4 times longer than for the regular frequency counter. Probably 4Hz is the absolute minimum speed (120 rpm for 2 imp/rev) which will give meaningful output, although I'd recommend you only use with 8Hz (240 rpm for 2 imp/rev) or higher.
While you could use a microphone, depending on your application a photodiode wired to the microphone input and an LED to form a beam-break (or a retro-reflective arrangement) might work better. The software allows you to choose from one to six impluses per revolution. Note if using multiple impulses per revolution then the impulses must be equally-spaced otherwise the program may fail to register a reliable reading.
Download: RevCounter1v3.exe
By downloading this file, you consent to the
standard disclaimer.
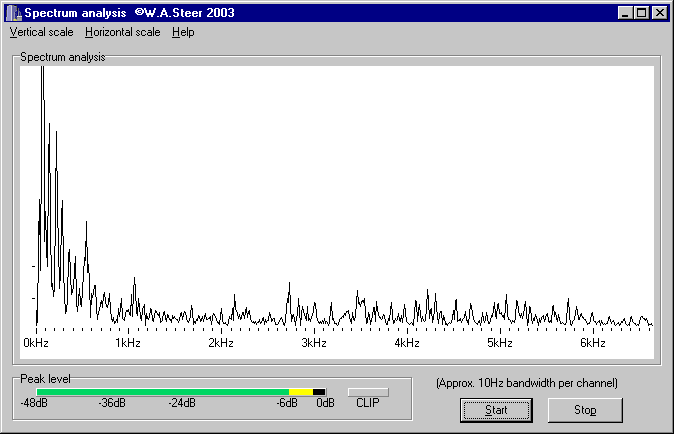
Having experimented with Fast Fourier Transforms (FFT) over the years, I realised that I could combine that routine with the sound sampling code sections to make a real-time audio spectrum analyser.
Like the other programs on this page, it uses the output from the 'Recording' mixer panel as its input.
Audio is sampled at 44.1kHz, with 16-bit resolution.
Please visit my dedicated Spectrum Analysis page at: specanaly.html for the downloads.
The dedicated page has current updates (e.g. Aug 2015) of the Spectrum Analysis with many more new features.
Example plot:
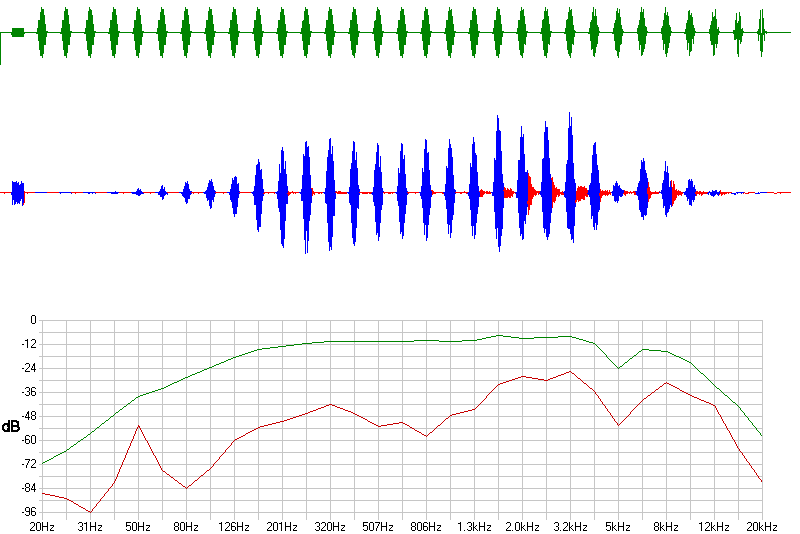
Test configuration:
The top (dark green) trace represents the outputted signal; 9-cycle cosine-enveloped, sinewave bursts at 20Hz, 25Hz, 31Hz, 40Hz,...20kHz (three tones per octave). Bursts are separated by a silence period of the same duration as the preceeding burst. The horizontal scale changes dynamically across the screen to make all bursts appear the same width!
The middle, blue and red, trace represents the received signal, again on a linear amplitude scale. The colouration is blue where a sound was expected, and red where it wasn't (in the outputted silence periods). 'Red' sounds arise primarily due to resonances in the microphone or speaker - but can also be caused by background noise in the room or electrical interference.
The bottom graph shows on a log (decibel) scale the amplitude of the received signal, after appropriate bandwidth filtering (green trace). The red trace below shows the amplitude of the received signal, similarly filtered, during the 'silence' periods - owing to background sounds etc, take the significance of this trace with a pinch of salt! It does show some sympathy with the resonances at 2-4kHz and 8kHz obvious in the red/blue received-signal plot. The peak at 50Hz is caused by AC mains electricity pickup.
Ideas for future development:
The program was also ran with the audio controls set for internal loopback. This showed that the electrical response was flat to within 3dB across the range 20Hz to 20kHz - but only when the soundcard bass and treble controls were set to one notch above minimum (on a scale of 1-7). With the controls in their mid position, there was a distinct dip of 6dB in the frequency response at around 1-2kHz - the region in between that affected by the tone controls!!!
Owing to its very experimental nature, this program is not available for download.
dB = 20 × log10 (A/Aref)
A ratio of 6dB corresponds to a factor of two change in signal amplitude, thus you get 6dB of 'dynamic range' for every bit of your ADC/DAC. Hence a 16-bit soundcard (or regular CD) has an intrinsic maximum dynamic range of 6dB × 16bits = 96dB. More specialist higher quality soundcards offer 24-bit sampling, and so 144dB of dynamic range - exceeding that of the human auditory system!
The charts on this program use the maximum obtainable amplitude (32768) as the reference (0dB) point.
Soundwaves travel at approximately 330 metres per second in air at room
temperature. If we placed a microphone beside a speaker, and facing a
wall 5 metres away, then made the speaker 'click', the microphone would
hear one click practically immediately (the direct sound), then an 'echo'
off the wall
2 ×5 / 330 = 0.0303 seconds later (the
factor of two arises because the sound has to travel to the wall and back,
making a total trip of 10 metres).
[You can clap your hands in front of a large exterior wall to test this.]
In practice, 'clicks' are not that good: among other problems, they can be difficult to distinguish from background noise. What is universally used in radar systems is a pseudo random bit sequence (PRBS) - in the case of sound, a hissing noise which contains all frequencies (up to a certain limit), with the special property that it only correlates (matches) with itself at time-offsets of zero (or the loop-period of the sequence - which can easily be made extremely long). If you have several echos, the received sequence will match a little at the time corresponding to each echo, but not at all in-between.
I wrote a program to sound a PRBS, and correlate the received signal from the microphone. It did work (sort of), and you could see the effect of objects placed up to a metre from the speaker/microphone - but even with no reflecting object, the direct correlation was not found to be 'clean'.
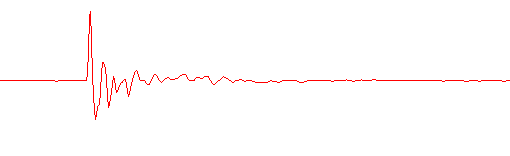
Direct correlation for microphone 3 inches in front of speaker
The problem was that resonances in the speaker and microphone were causing sound waves at certain frequencies to predominate. A single frequency will correlate with itself at time intervals which are multiples of the period, T, of each cycle. My 'multiple reflections' were separated by about 0.0003 seconds (0.3 milliseconds), indicating a system resonance at around 3.3kHz ( 1 / 0.0003 = 3333Hz ). There is also evidence of a resonance at around twice that frequency.
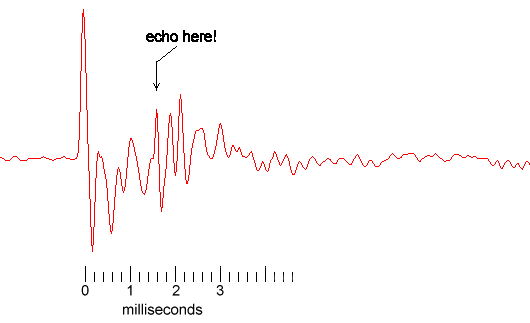
Early echo-plot
With the microphone and speaker side by side, and a hard object held about 0.3m in front of the speaker/mic, the above plot is seen. As well as the strong direct peak, there is a second echo peak (just discernable in the post-first-peak wobble) about 1.6 milliseconds later. That indicates a round-trip distance-difference of 330 × 0.0016 = 0.53m, an object distance of 0.53 / 2 = 0.26m. The slight underestimate can be explained by the small, but not insignificant, distance between the microphone and speaker!
This frustrating mess of overlapping peaks is what caused me to go back and investigate frequency response and resonances in the speaker-microphone system. By filtering out the offending frequency band in the transmitted and/or received sound, a cleaner echo-pattern should be obtainable...
With the sound routed via the internal loopback, (purely electrical, no actual acoustic waves) you get the following pattern - a good representation of a 'Kronecker delta' function.

Correlation for internal loopback (frequency response flat -3dB 20Hz-20kHz)
The spike goes down rather than up because some designer got an
inverting amplifier into the loopback path!
But if the soundcard's bass and treble controls are put in their "mid" positions (which we established before leaves a 6dB dip in the region of 1-2kHz -- see above) the pattern is as shown below.
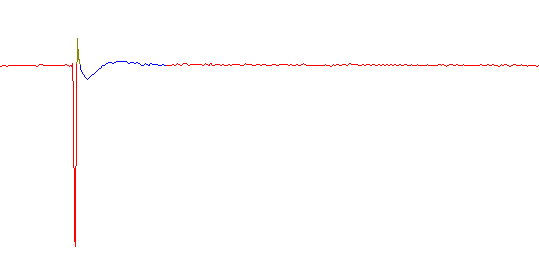
Correlation for internal loopback (bass and treble controls in "mid" positions).
The immediate overshoot (dark green) is caused by excess high-frequency (treble)
response, and the longer term wobble (blue) is caused by excess low-frequency (bass) response.
In fact, what the correlation function is showing is effectively the pulse-response of the system.
I have not yet managed to model the speaker/microphone response accurately enough to filter the signals to get clean acoustic correlation peaks. The response might turn out to be too bad to recover for this application...!
Consequently, with programs still undergoing development, they are not yet available for download.
I expanded this project to analyse an orchestral recording in terms of the musical notes present, and from the display was able to work out the music for prominant bits of the melody (not having a 'musical ear' I can't do that intuitively!).
"I reckon it should be possible to compress speech recordings down to rates of 1000bps (bits/sec) or less, and still keep it sounding 'natural'... it'll take some work though!"
Well, I've been rather busy this year - I did finish writing up my PhD thesis, get it printed, bound, passed the oral examination... and then started a new job.
I have still, particularly in the past few weeks (to 19 Nov 2001), been working on the groundwork for this challenge.
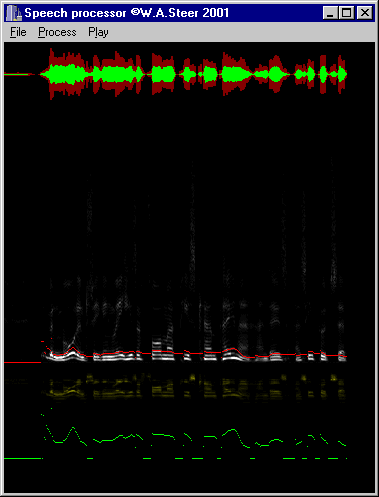
Latest speech-analysis program. The red and green bar at the top shows
the peak and RMS amplitude of the sound sample file as a function of time
(about 4 seconds total). The wavey greyscale lines is a frequency-spectra
versus time plot; one pixel represents approx. 43Hz vertically, and 1/86th
second horizontally. The yellow plot is also frequency spectra versus time,
but squashed onto a logarithmic frequency scale. The green wavey line at
the very bottom shows the tracking of the fundamental frequency with time,
and the red line superimposed on the main frequency/time plot represents the
third harmonic of the detected fundamental.
The program at present re-synthesises speech from a harmonic series of sine or cosine waves, varying the amplitudes according to the original signal (by a rough cludge using the Fourier spectrum).
Interestingly, the frequency of the fundamental has little bearing on the intelligibility of the speech, though making it constant turns the speech into plainsong, or making it track the original 'lazily' makes the speaker sound very tired.
Only once I've been able to track the amplitudes and separate the voiced from the unvoiced speech components properly, and can synthesise high quality speech reliably from its component parts, will I spend much time working out how best to discard information in order to achieve substantial compression...

©2001-2015 William Andrew Steer